Trong hình học, tam giác là một dạng hình cơ bản nhưng ẩn chứa nhiều yếu tố đặc biệt, trong đó có đường trung tuyến. Vậy đường trung tuyến là gì và có vai trò như thế nào trong việc phân tích hình học? Cùng tìm hiểu chi tiết khái niệm, đặc điểm và các ứng dụng thực tế của đường trung tuyến trong bài viết dưới đây.
Đường trung tuyến là gì trong tam giác?
Đường trung tuyến là đường gì? Trong hình học, đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, và ba đường này luôn cắt nhau tại một điểm duy nhất gọi là trọng tâm của tam giác.
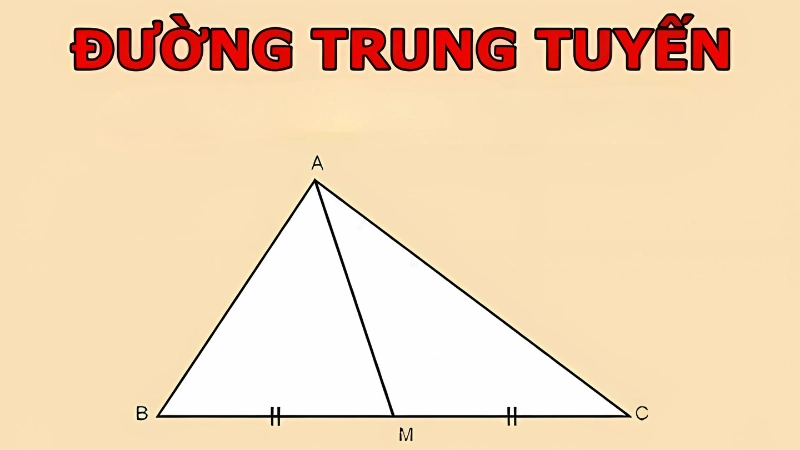
Ví dụ: Trong tam giác ABC, nếu M là trung điểm của cạnh BC thì đoạn thẳng AM chính là đường trung tuyến xuất phát từ đỉnh A.

Khái niệm “trung tuyến” xuất phát từ tính chất “trung điểm” của một cạnh và việc nối từ đỉnh đến điểm đó. Như vậy, mỗi đường trung tuyến đóng vai trò cân bằng hai phần của cạnh đối diện, đồng thời tạo nên các tính chất hình học thú vị cho tam giác.
Tóm lược:
- Đường trung tuyến là đường nối từ một đỉnh đến trung điểm của cạnh đối diện.
- Mỗi tam giác có ba đường trung tuyến.
- Ba đường trung tuyến cắt nhau tại trọng tâm.
>>>Đọc thêm: Còn cái nịt là gì? Nguồn gốc và ý nghĩa thực sự
Tính chất nổi bật của đường trung tuyến trong tam giác
Đường trung tuyến không chỉ là một khái niệm hình học đơn thuần mà còn mang nhiều tính chất đặc biệt, hỗ trợ hiệu quả trong việc giải bài tập và chứng minh.
Trọng tâm – Giao điểm của ba đường trung tuyến
Ba đường trung tuyến của một tam giác luôn cắt nhau tại một điểm duy nhất, được gọi là trọng tâm. Trọng tâm chính là tâm của khối lượng nếu tam giác là một vật thể đồng chất. Trọng tâm chia mỗi đường trung tuyến theo tỷ lệ 2:1, nghĩa là đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn từ trọng tâm đến trung điểm cạnh.
Ví dụ: Nếu G là trọng tâm của tam giác ABC, và M là trung điểm cạnh BC, thì:
- AM là đường trung tuyến.
- G nằm trên AM sao cho AG = 2GM.
Ứng dụng trong tính diện tích
Đường trung tuyến còn được ứng dụng trong công thức tính diện tích tam giác khi biết độ dài các cạnh. Đặc biệt, nếu biết độ dài ba trung tuyến, ta có thể áp dụng công thức trung tuyến để tính diện tích tam giác:
S=43sm(sm−ma)(sm−mb)(sm−mc)S = \frac{4}{3} \sqrt{s_m (s_m - m_a)(s_m - m_b)(s_m - m_c)}S=34sm(sm−ma)(sm−mb)(sm−mc)
Trong đó:
- ma,mb,mcm_a, m_b, m_cma,mb,mc là độ dài ba đường trung tuyến.
- sm=12(ma+mb+mc)s_m = \frac{1}{2}(m_a + m_b + m_c)sm=21(ma+mb+mc)
Trung tuyến trong tam giác vuông và đều
Trong tam giác đều, ba đường trung tuyến đồng thời là đường cao, đường phân giác và đường trung trực.
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Đây là một tính chất rất đặc biệt, giúp chứng minh và nhận diện tam giác vuông dễ dàng.
Vai trò của đường trung tuyến trong học tập và thực tế
Giúp phát triển tư duy hình học
Việc nắm vững khái niệm đường trung tuyến là gì không chỉ giúp học sinh giải các bài toán hình học nhanh hơn mà còn rèn luyện khả năng tư duy không gian, suy luận logic và kỹ năng chứng minh toán học. Đường trung tuyến xuất hiện nhiều trong đề thi học sinh giỏi, thi tốt nghiệp THPT và cả trong các kỳ thi đại học.
Liên kết với các yếu tố hình học khác
Đường trung tuyến không tồn tại đơn độc mà thường liên kết với các yếu tố hình học khác như:
- Đường cao
- Đường phân giác
- Trọng tâm
- Trung điểm
Những mối quan hệ này giúp tạo ra hệ thống lập luận chặt chẽ, hỗ trợ học sinh khi phân tích hình học phẳng.

Ứng dụng trong thực tế và kỹ thuật
Trong thực tế, đường trung tuyến mang ý nghĩa cân bằng trọng lượng. Trong thiết kế kỹ thuật, xây dựng hay kiến trúc, việc xác định trọng tâm vật thể (giao điểm các trung tuyến) giúp đảm bảo sự ổn định trong phân bố lực, trọng lượng. Chẳng hạn, trong xây cầu, xác định đúng trọng tâm sẽ giúp kết cấu bền vững hơn, hạn chế lệch tải.
>>>Đọc thêm: Cringe là gì? Giải mã hiện tượng gây ngượng chín mặt
Qua những phân tích trên, bạn đã hiểu rõ đường trung tuyến là gì, cách nhận biết, tính chất và tầm quan trọng của nó trong tam giác. Việc nắm vững kiến thức về đường trung tuyến sẽ giúp bạn giải bài tập hình học dễ dàng hơn và phát triển tư duy không gian logic, đặc biệt khi học toán nâng cao hay ôn thi.


