Trong chương trình toán học phổ thông, đặc biệt là hình học lớp 7 và lớp 9, học sinh sẽ gặp nhiều điểm đặc biệt của tam giác như trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp. Trong số đó, trực tâm là gì là câu hỏi được nhiều người đặt ra khi học đến phần tam giác và đường cao. Vậy trực tâm có vai trò như thế nào và cách xác định nó ra sao? Bài viết sau sẽ giải đáp toàn bộ những thắc mắc xoay quanh khái niệm này.
Trực tâm tam giác là gì?
Trực tâm của tam giác là gì? Đây là khái niệm chỉ điểm chung của ba đường cao trong một tam giác. Mỗi đường cao của tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện (hay phần kéo dài của cạnh đó). Khi kẻ đầy đủ ba đường cao trong một tam giác, chúng sẽ cùng cắt nhau tại một điểm duy nhất – đó chính là trực tâm.
Cụ thể hơn, nếu ta có một tam giác ABC, các đường cao từ A, B và C lần lượt là AD, BE và CF (vuông góc với cạnh BC, AC và AB), thì ba đường này sẽ cắt nhau tại một điểm H. Điểm H chính là trực tâm của tam giác ABC.

Các tính chất cơ bản của trực tâm
Trực tâm luôn nằm trên giao điểm của ba đường cao trong tam giác.
Tùy vào dạng tam giác, vị trí của trực tâm có thể thay đổi:
- Với tam giác nhọn, trực tâm nằm bên trong tam giác.
- Với tam giác vuông, trực tâm chính là đỉnh của góc vuông.
- Với tam giác tù, trực tâm nằm bên ngoài tam giác.
Khái niệm trực tâm tam giác là gì không chỉ đơn thuần là học thuộc lòng mà còn là cơ sở để giải quyết các bài toán hình học phức tạp hơn như chứng minh đồng quy, tính toán độ dài, hoặc sử dụng trong các bài toán quỹ tích.
>>>Khám phá ngay: Cringe là gì? Giải mã hiện tượng gây ngượng chín mặt
Trực tâm là giao điểm của ba đường gì?
Một trong những câu hỏi phổ biến khi tìm hiểu về trực tâm là: Trực tâm là giao điểm của ba đường gì? Câu trả lời ngắn gọn và chính xác là: trực tâm là giao điểm của ba đường cao trong tam giác.
Ba đường cao được xác định như sau:
- Từ mỗi đỉnh của tam giác, kẻ một đường vuông góc với cạnh đối diện.
- Mỗi đường cao sẽ cắt một cạnh (hoặc phần kéo dài của cạnh đó) tại một điểm vuông góc.
- Ba đường cao này luôn đồng quy tại một điểm – đó là trực tâm.
Điểm đặc biệt ở đây là dù bạn chỉ cần kẻ hai đường cao, giao điểm của chúng cũng sẽ nằm trên đường cao thứ ba. Điều này giúp chúng ta dễ dàng xác định trực tâm mà không cần phải kẻ cả ba đường cao.
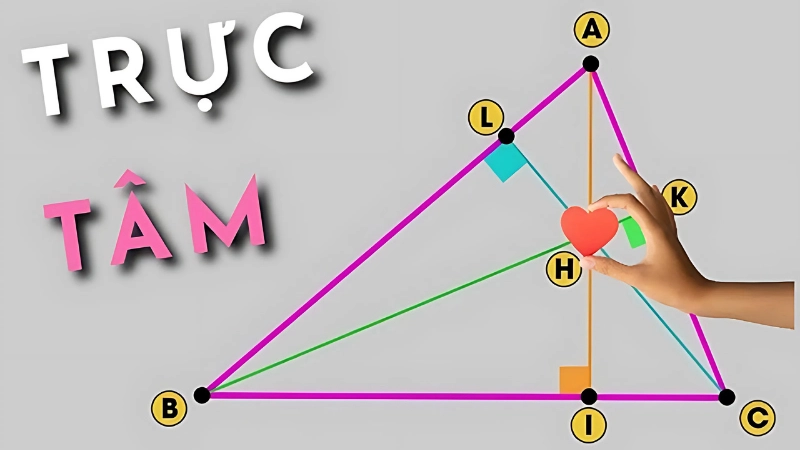
Cách xác định trực tâm của tam giác
Để hiểu rõ hơn về khái niệm trực tâm của tam giác là gì, ta cần nắm vững cách xác định trực tâm trên thực tế. Dưới đây là một số bước cơ bản:
Bước 1: Vẽ tam giác
Giả sử bạn có tam giác ABC. Hãy vẽ tam giác bất kỳ (nhọn, vuông hoặc tù) tùy theo yêu cầu bài toán.
Bước 2: Kẻ hai đường cao
Chọn hai đỉnh của tam giác, ví dụ A và B. Từ điểm A, kẻ một đường vuông góc với cạnh BC. Tương tự, từ điểm B kẻ một đường vuông góc với cạnh AC.
Bước 3: Tìm giao điểm
Giao điểm của hai đường cao vừa kẻ chính là trực tâm H của tam giác ABC. Để kiểm chứng, bạn có thể kẻ đường cao thứ ba từ đỉnh C và thấy rằng nó cũng đi qua điểm H này.
Một số lưu ý:
- Nếu tam giác là tam giác nhọn, các đường cao nằm trong tam giác.
- Nếu là tam giác tù, bạn cần kéo dài cạnh đối diện để vẽ đường cao.
- Trong tam giác vuông, đường cao từ góc vuông trùng với cạnh góc vuông, do đó trực tâm nằm ngay tại đỉnh đó.
Vai trò và ứng dụng của trực tâm trong toán học
Việc hiểu rõ trực tâm tam giác là gì sẽ giúp ích rất nhiều trong học tập và giải toán hình học. Dưới đây là một số vai trò và ứng dụng cụ thể:
Giải bài toán hình học phẳng
Trong các đề toán thi học sinh giỏi, toán nâng cao hoặc toán hình lớp 9, trực tâm thường được sử dụng để chứng minh đồng quy, chứng minh hai đoạn thẳng vuông góc hoặc để tính độ dài các đoạn thẳng.
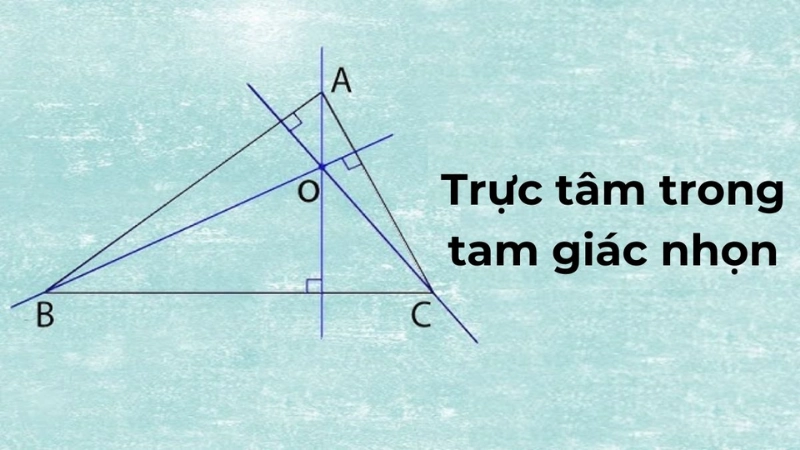
Ví dụ: Cho tam giác ABC có trực tâm H, chứng minh rằng ba điểm H, trung điểm cạnh BC và tâm đường tròn ngoại tiếp ABC thẳng hàng.
Dùng trong hình học tọa độ
Trong hình học tọa độ Oxy, trực tâm có thể được tìm bằng cách viết phương trình các đường cao và tìm giao điểm của chúng. Đây là cách phổ biến để giải toán chính xác bằng đại số.
Giúp hiểu sâu hơn về các điểm đặc biệt
Ngoài trực tâm, một tam giác còn có các điểm đặc biệt khác như trọng tâm (giao ba đường trung tuyến), tâm đường tròn nội tiếp (giao ba phân giác), và tâm đường tròn ngoại tiếp (giao ba đường trung trực). Việc hiểu trực tâm giúp học sinh hệ thống kiến thức tốt hơn, phân biệt rõ ràng giữa các điểm đặc biệt này.
>>>Khám phá ngay: Đường trung tuyến là gì và cách xác định chính xác
Qua bài viết, chắc hẳn bạn đã hiểu rõ trực tâm là gì và cách xác định nó trong tam giác. Việc nắm vững kiến thức về trực tâm không chỉ giúp học tốt môn Toán mà còn phát triển tư duy logic và hình học không gian. Hãy luyện tập thêm các bài toán có sử dụng trực tâm để củng cố kỹ năng vẽ hình và phân tích tam giác hiệu quả hơn.


